
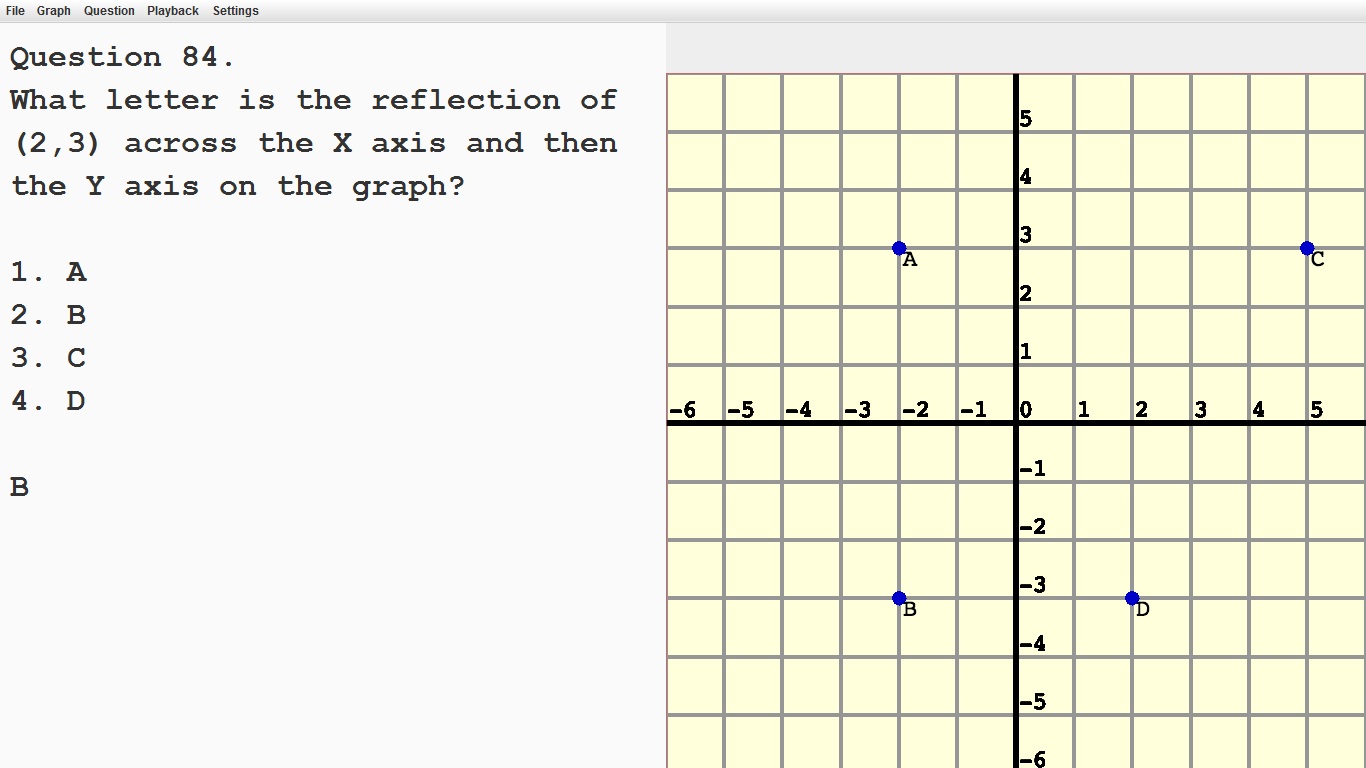
This will involve changing the coordinates.įor example, try to reflect over the -axis. Reflection of Functions over the x-axis and y-axis Reflecting a function over the x -axis and y -axis. Reflection over the x-axis is a type of linear transformation that flips a shape or graph over the x-axis. In this lesson, we’ll go over reflections on a coordinate system. Do the same for the other points and the points are also Count two units below the x-axis and there is point A’. As a result, points of the image are going to be:īy counting the units, we know that point A is located two units above the x-axis. Since the reflection applied is going to be over the x-axis, that means negating the y-value. Determine the coordinate points of the image after a reflection over the x-axis. Triangle ABC with coordinate points A(1,2), B(3,5), and C(7,1). For example, if a point ( 3, 7) is present in the first quadrant and we reflect it over the y-axis, then the resulting point will be ( 3, 7). You can also negate the value depending on the line of reflection where the x-value is negated if the reflection is over the y-axis and the y-value is negated if the reflection is over the x-axis.Įither way, the answer is the same thing. Reflection Over Y-axis When we reflect a figure or polygon over the y-axis, then the y-coordinates of all the vertices of the polygon will remain the same while the sign of the x-coordinates will change. To match the distance, you can count the number of units to the axis and plot a point on the corresponding point over the axis. (You can view the solution by clicking on the problem.To reflect a shape over an axis, you can either match the distance of a point to the axis on the other side of using the reflection notation. Similarly when we reflect a point (p,q) over the y-axis the y-coordinate stays the same but the x-coordinate changes signs so the image is (-p,q). You can use the rule or count towards the reflection line. This video shows two methods of achieving this reflection. Use reflections and rescalings (followed by shifts) to graph the following functions. This video demonstrates the steps needed to reflect a figure over the y-axis. Rescalings and reflections (interchangeable).We are left with an order of function transformations, similar to the concept of order of operations in arithmetic, but different in actual order: However, when dealing with reflections and shifts simultaneously, it’s important to perform horizontal shifts first, then reflections, and lastly vertical shifts. Likewise, when dealing with reflections and rescalings simultaneously, it doesn’t matter which we perform first. When we have both vertical and horizontal reflections, it doesn’t matter which we perform first. To reflect over a vertical line, such as x a, first translate so the line is shifted to the y-axis, then reflect over it, then translate back so the line is shifted to its original position. where a, b, c are coefficients of the line and x and y is the coordinates of your given point. If the pre-image is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C'. We can get the perpendicular distance from the point tk the line by : ax + by + c a2 + b2. The original object is called the pre-image, and the reflection is called the image. On the other hand, if the negative is inside the function, then the input x-value switches sign, essentially reflecting every point over the y-axis. A reflection can be done across the y-axis by folding or flipping an object over the y axis. If the negative is outside the function, then the output y-value switches sign, essentially reflecting every point over the x-axis. each corner with letters, and to use a little dash (called a Prime) to mark each corner of the reflected image. The intuition behind reflections is that, depending where it is placed, the negative sign switches positive and negative values of the $x$ or $y$ variable. Reflections occur when a function is made negative – when the negative is outside the function, the reflection is over the y-axis and when the negative is inside the function, the reflection is over the x-axis. A vertical reflection reflects a graph vertically across the x -axis, while a horizontal reflection reflects a graph horizontally across the y -axis.
When a function is reflected, it flips across one of the axes to become its mirror image. Another transformation that can be applied to a function is a reflection over the x or y -axis.


 0 kommentar(er)
0 kommentar(er)
